Main Menu
- Home
- Product Finder
- Calibration Systems
- Calibration Services
- Digital Sensing
- Industrial Vibration Calibration
- Modal and Vibration Testing
- Non-Destructive Testing
- Sound & Vibration Rental Program
- Learn
- About Us
- Contact Us
The Modal Shop’s General Purpose vibration shakers are a proven solution for your vibration testing applications. With force ratings of 7, 40, 75, and 110 lbf; these dual purpose shakers are suitable for both structural testing and modal applications. But before testing can begin, select a vibration shaker suited to your testing needs by answering the questions below. Click each question for step by step instructions.
Add the following masses:
test item + any adaptors & fixtures = payload
Adaptors and fixtures are sometimes required to mount the test item as it is not possible to drill additional holes in the shaker armature. Components, cables, connectors, and bolts, that move with the shaker during testing must be included in the total weight.
If you do not know the acceleration required for testing, convert your vibration specification data into acceleration units. Use g's peak for sine testing or g's rms for random testing.
English calculations: 1 g = 32.2 ft/s²
Metric calculations: 1g = 9.8 m/s²
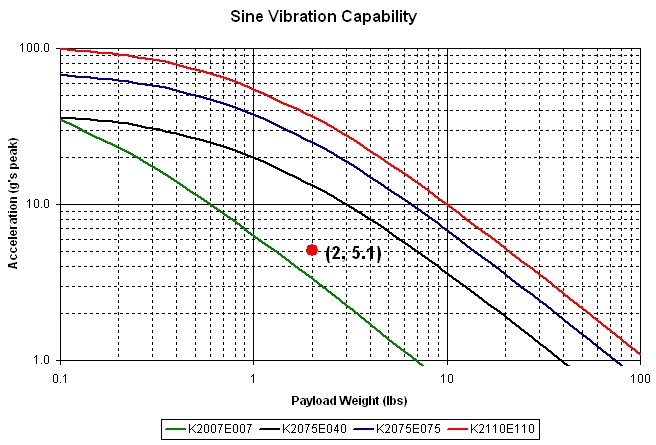
Any vibration shaker with a sine curve above your point of intersection will serve the basic functions required for testing.
Check for the frequencies required on your test to verify that you will not exceed the shaker's stroke capability. Using the minimum frequency and acceleration levels, calculate the displacement using the following equations:
English calculations: 19.56 g/f² = d [inches pk-pk]
Metric calculations: 496.82 g/f² = d [millimeters pk-pk]
To ensure you are within the shaker's stroke capacity, displacement should be less than:
0.5 in / 12.7 mm for model K2007E007
1 in / 25.4 mm for models K2075E040, K2075E075 and K2110E110
1. Payload
The test item has a mass of 1.5 lbs and the necessary adaptors have a mass of 0.5 lb
1.5 + 0.5 = 2.0 lbs payload
2. Required Acceleration
The test will be performed at an acceleration of up to 50 m/s². To find the g's required for testing:
(50 m/s²) / (9.8 m/s²) = 5.1 g's
3. Intersection on Graph
By plotting the intersection of 5.1 g's and 2.0 lbs on the graphs, you will see that the K2075E040, K2075E075, and K2110E110 all provide the necessary capabilities for testing.
4. Low Frequency Displacement Requirements
Assuming we want to use the K2075E040 or the K2110E110 shakers, the maximum stroke is equal to 1 inch. Applying the equation above, 19.56 g/f² should be less than or equal to one
inch.
19.56 g/f² = 19.56(5.1)/f² = 99.76/f²
99.76/f² < 1 so f²=9 9.76
√
99.76 = 9.99 so f > 9.9 Hz
The selected shakers will allow testing down to 9.9 Hz before vibration levels must be altered.